FOR DEVELOPERS
Differences Between Network Analysis and Geometric Deep Learning on Graphs
How do social networking platforms like Facebook and Instagram generate friend or follower suggestions? What’s more, we tend to know many of these suggestions. A common technology used for this is network analysis.
This article will explore network analysis and geometric deep learning in detail and examine the differences between them.
What is a network?
A network is a symbolic representation of the essential characteristics of a group of objects/people. It is also known as a graph in mathematics.
Let’s understand this better with an example: say you’re a project manager and are asked to use four machines with the help of two men. What do you do? You try to figure out how to make the most out of the men by drafting a schedule detailing what time they will work and on which machines. You then need to check if the work assigned is being performed to par. All this seems like a lot of effort and it is. One way to save time is with the help of networks. Look at the following diagram:
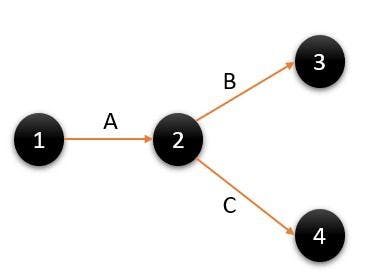
Image source: Author
Image source: Author
Here, the arrows are known as ‘edges’ and represent the relationships between the objects and the circles, known as ‘vertices’ or ‘nodes’. They represent the objects we will analyze. In this way, we can create a network to make work easier.
For example, if we study a social relationship between Instagram users, nodes will be the target users and edges will be the relationship, such as the friendships between users.
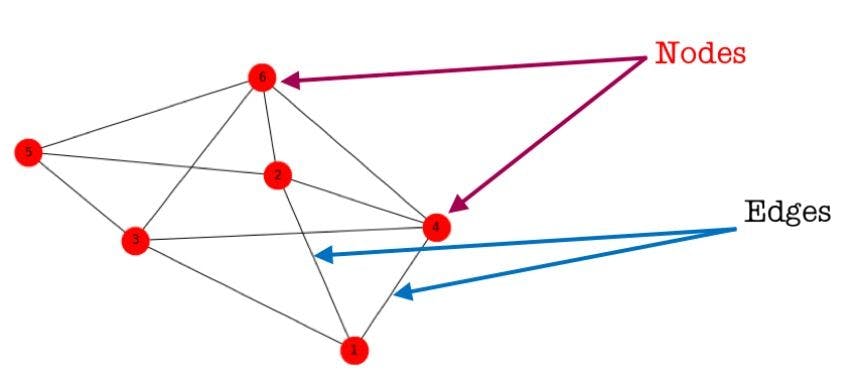
Why do we need network analysis?
Network analysis is beneficial for many applications. It helps in understanding the complex relationships in social networks or in analyzing the biological systems of organisms. It also helps in comprehending networks like those in banking, airlines, and supply chain. Here’s how:
- In a social network, network analysis helps identify the most influential person in the group.
- In airlines' networks, it can identify the fuel usage or distance covered.
- In banking networks, it can help recognize the type, amount, time, and location of transactions.
- In supply chain networks, it can ascertain the load capacity, year of manufacture, maintenance cost, etc.
What is geometric deep learning?
Geometric deep learning was first introduced by Bronstein et al in their 2017 paper titled ‘Geometric Deep Learning: Going beyond Euclidean data’. It is defined as “an umbrella term for emerging techniques attempting to generalize (structured) deep neural models to non-Euclidean domains, such as graphs and manifolds”.
Geometric deep learning posits i) whether we can give the world a base where different architectures like convolutional neural networks (CNNs), recurrent neural networks (RNNs), transformers, etc. can have a common mathematical framework, and ii) if we can have certain prior physical knowledge that can be embedded in any architecture.
A new field of ML, geometric deep learning can learn from complex data like graphs and multi-dimensional points. In recent years, algorithms like CNN, long short-term memory (LSTM), generative adversarial network (GAN), etc. have helped achieve amazing accuracy on different types of problems.
Euclidean and non-euclidean spaces
According to Wikipedia, “A Euclidean space is a finite-dimensional vector space over the reals R, with an inner product”. Simply put, it involves the functional of 1D, 2D to n number of dimensions.
Euclidean looks for a flat surface whereas non-Euclidean looks for a curved surface. Some examples of non-Euclidean space are graphs/networks, manifolds, and similar complex structures. A few examples of Euclidean space are text, audio, images, etc.
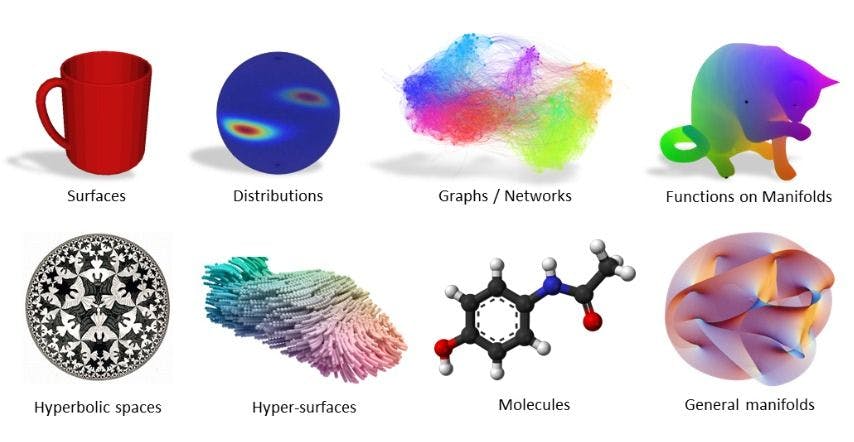
Many algorithms used in ML applications are old and only work on Euclidean data. There is also a wide range of 3D-shaped representations, one of which is manifolds. These can be explained as multi-dimensional spaces. Here, a shape composed of any point is represented by a single point in this new space, and similar shapes are close to each other.
In order to apply deep neural networks on these types of datasets, it’s imperative to use other techniques by keeping the limits of non-Euclidean data in mind. These are:
- No common system of coordinates
- No vector space structure
- No shift variant
Why do we need geometric deep learning?
A problem with learning in higher dimensions is that as the dimensions increase, so does the volume. For instance, if a solid ball is taken to infinite dimensions, the volume will shift from the center to the circumference and the ball will become hollow. But, if the ball is brought into a lower dimension, the sphere will be refilled. What this implies is that higher dimensional data is sparse and it becomes difficult to learn from sparse data.
Owing to this sparsity, one cannot find something that is close to the other dataset. However, geometric deep learning takes advantage of the fact that most tasks or functions that need to be estimated have underlying regularities through geometric principles in lower dimensions.
Another problem with graph-structured data is that standard deep neural networks are not able to interpret or learn it. This is because most networks are based on convolutions, which run smoothly on Euclidean data. As mentioned, datasets like graphs, manifolds, etc. are considered non-Euclidean data, meaning that they do not have shift-invariance and a common system of coordinates.
In order to deal with these problems and generalize deep neural networks to non-Euclidean domains, geometric deep learning has emerged as a separate research field.
Differences between network analysis and geometric deep learning
Network analysis
- Does not use deep learning techniques, and focuses on understanding the structure of a network.
- Provides a better way of dealing with theoretical concepts like relationships and interactions.
- Used to study social networks, physician networks, supply chain networks, etc. Out of all of them, the social network is probably the best-known application of graphs in data science.
- Some of the metrics used in networks to understand their properties are centrality, modularity, assortative, etc.
Geometric deep learning
- Uses deep learning techniques on non-Euclidean datasets.
- Directed more towards using datasets structured as graphs or networks as an input to deep learning problems like regression.
- Some of the main areas of research are graph representation and neural architecture.
Moving from two to three-dimensional volumes is essential for the future of deep learning. It would allow technology to achieve efficiency closer to the human brain using machine learning and deep learning techniques. Due to the increase in non-Euclidean data, geometric deep learning is gaining more ground. Through it, technology can match billions of atoms to track down new drug options to treat existing diseases, for example. This may be particularly useful in situations where chronic diseases are difficult to treat.
